One of Neptune's core components is Triton Virtual Machine. Its associated engine for Zero-Knowledge Succinct Transparent Arguments of Knowledge (zk-STARKs) allows proving correct program execution. Neptune uses Triton VM to check the chain's consensus logic, among other tasks. This allows proving that all necessary checks have been performed successfully. The generated proof is part of the reason the Neptune chain stays small in size for all full nodes.¹

Zk-STARKs are fascinating technology. Unfortunately, they are also somewhat complex.² Creating multiple but manageable pieces is a common strategy to tackle complex matters. Triton VM is no different: While an intricate machinery when taken as a whole, it consists of distinct parts with clear roles. For example, the hash coprocessor's only task is to perform hashing operations. Similarly, the RAM unit's sole responsibility is guaranteeing memory consistency. Because of the way STARKs work, a crucial ingredient for any part of Triton VM is its associated table, which you can imagine as a spreadsheet. Even though they are distinct, the various parts have to work together to make the proof generated by Triton VM a convincing one. In other words, the tables have to be linked together somehow.

Figure 1 Two tables as used in Triton VM. Without an argument linking the tables, the Processor Table on the left is completely disconnected from the RAM Table on the right.

In Triton VM, there are 3 different ways to link tables together:

1. Permutation Arguments establish that two lists $A = (a_0, \dots, a_n)$ and $B = (b_0, \dots, b_n)$ are permutations of each other.
2. Evaluation Arguments establish that two lists $A = (a_0, \dots, a_n)$ and $B = (b_0, \dots, b_n)$ are identical.
3. Lookup Arguments establish that all elements of list $A = (a_0, \dots, a_\ell)$ also occur in list $B = (b_0, \dots, b_n)$.

All methods are cryptographic arguments relying on equality of polynomials or rational functions. This allows using the Schwartz-Zippel lemma to efficiently check those equalities.³ The precise nature of the polynomials or rational functions in question differs between the 3 arguments, and dictate the link's properties.

Compressing Multiple Elements

Mathematically, all arguments used in Triton VM are about single elements of the finite field $\mathbb{F}_p$ where $p = 2^{64} - 2^{32} + 1$. In practice, it is very useful to argue about multiple elements. A common trick is to “compress” multiple elements into a single one using random weights. These weights are “supplied by the STARK verifier,” i.e., sampled using the Fiat-Shamir heuristic after the prover has committed to the elements in question. For example, if $a$, $b$, and $c$ are to be incorporated into the cryptographic argument, then the prover

• commits to $a$, $b$, and $c$,
• samples weights $\alpha$, $\beta$, and $\gamma$ using the Fiat-Shamir heuristic,
• “compresses” the elements in question to $\delta = \alpha\cdot a + \beta\cdot b + \gamma\cdot c$, and
• uses $\delta$ in the cryptographic argument.

In the following, all cryptographic arguments are presented using single field elements. Depending on the use case, this single element represents multiple, “compressed” elements.

Permutation Argument

To create a link establishing that $A$ is a permutation of $B$, the lists' elements are interpreted as the roots of polynomials $f_A(X)$ and $f_B(X)$, respectively:

$$ f_A(X) = \prod_{i=0}^n X - a_i \qquad\qquad f_B(X) = \prod_{i=0}^n X - b_i $$

The two lists $A$ and $B$ are a permutation of each other if and only if the two polynomials $f_A(X)$ and $f_B(X)$ are identical. In Triton VM, the Permutation Argument is generally applied to show that the rows of one table appear in some other table without enforcing the rows' order in relation to each other. To establish this, the prover

• commits to the base column in question,
• samples a random challenge $\alpha$ through the Fiat-Shamir heuristic,
• computes the running product of $f_A(\alpha)$ and $f_B(\alpha)$ in the respective tables' extension column.

For example:

base column A	extension column A: running product		base column B	extension column B: running product
0	$(\alpha - 0)$		2	$(\alpha - 2)$
1	$(\alpha - 0)(\alpha - 1)$		1	$(\alpha - 2)(\alpha - 1)$
2	$(\alpha - 0)(\alpha - 1)(\alpha - 2)$		3	$(\alpha - 2)(\alpha - 1)(\alpha - 3)$
3	$(\alpha - 0)(\alpha - 1)(\alpha - 2)(\alpha - 3)$		0	$(\alpha - 2)(\alpha - 1)(\alpha - 3)(\alpha - 0)$

Another example of a (subset) Permutation Argument can be found between Triton VM's U32 Table and Processor Table.

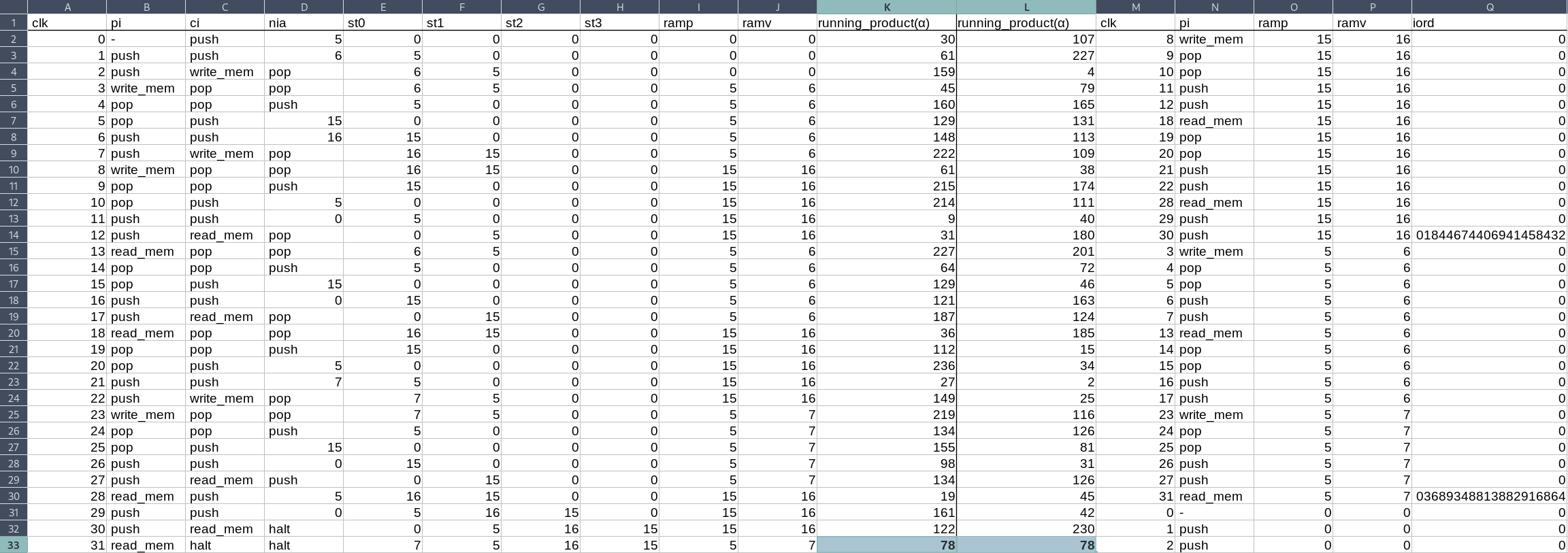Figure 2 A Permutation Argument establishes that the rows of the Processor Table were correctly copied to the RAM Table.

Evaluation Argument

To create a link establishing that $A$ is identical to $B$, the lists' elements are interpreted as the coefficients of polynomials $f_A(X)$ and $f_B(X)$, respectively:

$$ f_A(X) = X^{n+1} + \sum_{i=0}^n a_{n-i}X^i \qquad\qquad f_B(X) = X^{n+1} + \sum_{i=0}^n b_{n-i}X^i $$

The two lists $A$ and $B$ are identical if and only if the two polynomials $f_A(X)$ and $f_B(X)$ are identical. In Triton VM, the Evaluation Argument is generally used to show that (parts of) some row appear in two tables in the same order. To establish this, the prover

• commits to the base column in question,
• samples a random challenge $\alpha$ through the Fiat-Shamir heuristic,
• computes the running evaluation of $f_A(\alpha)$ and $f_B(\alpha)$ in the respective tables' extension column.

For example, in both Table A and B:

base column	extension column: running evaluation
0	$\alpha^1 + 0\alpha^0$
1	$\alpha^2 + 0\alpha^1 + 1\alpha^0$
2	$\alpha^3 + 0\alpha^2 + 1\alpha^1 + 2\alpha^0$
3	$\alpha^4 + 0\alpha^3 + 1\alpha^2 + 2\alpha^1 + 3\alpha^0$

More examples for (subset) Evaluation Arguments can be found between Triton VM's Hash Table and Processor Table.

Lookup Argument

Of the three, the Lookup Argument is the most complex one. It creates a link establishing that the elements being looked up, contained in $A$, appear in a lookup table, $B$. Both lists $A$ and $B$ may contain duplicates. However, it is inefficient if $B$ does, and is therefore assumed not to.

The example at the end of this section summarizes the necessary computations for the Lookup Argument. The rest of the section derives those computations. The first step is to interpret both lists' elements as the roots of polynomials $f_A(X)$ and $f_B(X)$, respectively:

$$ f_A(X) = \prod_{i=0}^\ell X - a_i \qquad\qquad f_B(X) = \prod_{i=0}^n X - b_i $$

By counting the number of occurrences $m_i$ of unique elements $a_i \in A$ and eliminating duplicates, $f_A(X)$ can equivalently be expressed as:

$$ f_A(X) = \prod_{i=0}^n (X - a_i)^{m_i} $$

The next step uses

• the formal derivative $f'_A(X)$ of $f_A(X)$, and
• the multiplicity-weighted formal derivative $f'^{(m)}_B(X)$ of $f_B(X)$.

The former is the familiar formal derivative:

$$ f'_A(X) = \sum_{i=0}^n m_i (X - a_i)^{m_i - 1} \prod_{j \neq i}(X - a_j)^{m_j} $$

The multiplicity-weighted formal derivative uses the lookup-multiplicities $m_i$ as additional factors:

$$ f'^{(m)}_B(X) = \sum_{i=0}^n m_i \prod_{j \neq i}(X - b_j) $$

Let $g(X)$ the greatest common divisor of $f_A(X)$ and $f'_A(X)$. The polynomial $f_A(X) / g(X)$ has the same roots as $f_A(X)$, but all roots have multiplicity 1. This polynomial is identical to $f_B(X)$ if and only if all elements in list $A$ also occur in list $B$.

A similar property holds for the formal derivatives: The polynomial $f'_A(x) / g(X)$ is identical to $f'^{(m)}_B(X)$ if and only if all elements in list $A$ also occur in list $B$. By solving for $g(X)$ and equating, the following holds:

$$ f_A(X) \cdot f'^{(m)}_B(X) = f'_A(X) \cdot f_B(X) $$

Optimization through Logarithmic Derivatives

The logarithmic derivative of $f(X)$ is defined as $f'(X) / f(X)$. Furthermore, the equality of monic polynomials $f(X)$ and $g(X)$ is equivalent to the equality of their logarithmic derivatives. This allows rewriting above equation as:

$$ \frac{f'_A(X)}{f_A(X)} = \frac{f'^{(m)}_B(X)}{f_B(X)} $$

Using logarithmic derivatives for the equality check decreases the computational effort for both prover and verifier. Concretely, instead of four running products – one each for $f_A$, $f'_A$, $f_B$, and $f'^{(m)}_B$ – only two logarithmic derivatives are needed. Namely, considering once again list $A$ containing duplicates, above equation can be written as:

$$ \sum_{i=0}^\ell \frac{1}{X - a_i} = \sum_{i=0}^n \frac{m_i}{X - b_i} $$

To compute the sums, the lists $A$ and $B$ are base columns in the two respective tables. Additionally, the lookup multiplicity is recorded explicitly in a base column of the lookup table.

For example:

base column A	extension column A: logarithmic derivative		base column B	multiplicity	extension column B: logarithmic derivative
0	$\frac{1}{\alpha - 0}$		0	1	$\frac{1}{\alpha - 0}$
2	$\frac{1}{\alpha - 0} + \frac{1}{\alpha - 2}$		1	1	$\frac{1}{\alpha - 0} + \frac{1}{\alpha - 1}$
2	$\frac{1}{\alpha - 0} + \frac{2}{\alpha - 2}$		2	3	$\frac{1}{\alpha - 0} + \frac{1}{\alpha - 1} + \frac{3}{\alpha - 2}$
1	$\frac{1}{\alpha - 0} + \frac{2}{\alpha - 2} + \frac{1}{\alpha - 1}$
2	$\frac{1}{\alpha - 0} + \frac{3}{\alpha - 2} + \frac{1}{\alpha - 1}$

Another example for a Lookup Argument can be found between Triton VM's Program Table and Processor Table.

Conclusion

Triton VM is a complex machine. Breaking it down into distinct parts helps conquer the complexity. However, if left in isolation, the various parts do not aid the overall machine, and generated proofs are not convincing. Therefore, the parts are linked together through a variety of cryptographic arguments. The argument is chosen based on the properties required of the link: Permutation Arguments establish that two lists contain the same elements in arbitrary order, Evaluation Arguments establish that two lists are identical, and Lookup Arguments establish that all the elements of one list also appear in some other list.

---